Kontakt

Astronomia-on-net

Najdete nás aj na fb.com

0908087986

Úvodná stránka > Všeobecná teoria relativity

Všeobecná teoria relativity

13.11.2012 20:58

Všeobecná teória relativity je teória o priestore, čase a gravitácii, ktorú sformuloval Albert Einstein v rokoch 1911 až 1916 (zverejnená bola v roku 1916).

Opisuje vzájomné pôsobenie (interakciu) priestoru a času na jednej strane a hmoty (vrátane polí) na strane druhej. Jej hlavná výpoveď je, že gravitácia vlastne nie je nič iné ako geometrický jav v zakrivenom štvorrozmernom časopriestore, presnejšie: Hmotné telesá sú zdrojom gravitačného poľa, ktoré určuje metriku (vlastnosti) časopriestoru v danej oblasti, ktorá zas naopak spätne ovplyvňuje stav a pohyb telies v danej oblasti.

Niektoré vlastnosti:

Teória aplikuje princíp relativity na oblasti, v ktorých má rozhodujúcu úlohu gravitácia.
Jej základom je princíp ekvivalencie.

Všeobecná teória relativity je rozšírením špeciálnej teórie relativity a pre dostatočne malé oblasti časopriestoru sa s ňou stáva identickou. V porovnaní so špeciálnou teóriou relativity je pre laika oveľa ťažšie zrozumiteľná, existuje však pre ňu dostatočné množstvo experimentálnych dôkazov.

Gravitácia a zakrivenie priestoru

Dvojrozmerné zobrazenie zakrivenia časopriestoru. Prítomnosť hmoty mení geometriu časopriestoru a táto (zakrivená) geometria je interpretovaná ako gravitácia.

Všeobecná teória relativity vyvodzuje gravitáciu z geometrického javu v zakrivenom časopriestore, pretože konštatuje:

Hmota (presnejšie jej energia a hybnosť) zakrivuje časopriestor vo svojom okolí.
Predmet, na ktorý nepôsobí žiadna sila, sa pohybuje medzi dvoma miestami časopriestoru vždy po najpriamočiarejšiej trajektórii, takzvanej geodetickej čiare.

Prvá výpoveď opisuje pôsobenie energie a hybnosti na časopriestor, druhá naopak – ide teda o vzájomné pôsobenie (interakciu) v pravom slova zmysle.

Už štvorrozmerný časopriestor špeciálnej teórie relativity sa dá ťažko názorne predstaviť - pri zakrivenom časopriestore je to o to ťažšie. V záujme predstavivosti si však možno pozrieť situácie so zníženým počtom rozmerov. Napríklad v prípade dvojrozmernej zakrivenej krajiny zodpovedá najpriamejšiej trajektórii, ktorú by prešlo vozidlo s riadením zafixovaným na jazdu rovno vpred. Ak by dve takéto vozidlá odštartovali na rovníkuparalelne smerom na sever, stretli by sa na severnom póle. Pozorovateľ, ktorý by nevedel o guľovom tvareZeme, by z toho vyvodil, že medzi dvomi vozidlami existuje príťažlivá sila. V skutočnosti ide o geometrický jav (guľatosť Zeme). Gravitačné sily sa preto niekedy označujú aj ako zdanlivé sily.

[upraviť]Princíp ekvivalencie

Keďže najpriamejšia dráha časopriestorom prirodzene nezávisí od hmotnosti, padajú všetky telesá v gravitačnom poli rovnako rýchlo, čo zistil už Galileo Galilei. Túto okolnosť vysvetľuje newtonovská mechanika princípom ekvivalencie (= gravitačná hmotnosť a zotrvačná hmotnosť telesa sú si rovné), ktorý týmto vlastne všeobecnú teóriu relativity vysvetľuje. Presnejšie možno povedať, že z klasického princípu ekvivalencie vyplýva, že pozorovateľ v uzavretom priestore bez pozorovania okolia nedokáže z pohybu predmetov v priestore zistiť, či je v stave beztiaže alebo voľného pádu. Einstein tento princíp zovšeobecnil takto: Pozorovateľ v uzavretom priestore bez informácií zvonku nemôže vôbec žiadnym pokusom zistiť, či je v stave beztiaže alebo nie.

[upraviť]Hodiny v gravitačnom poli

Vo všeobecnej teórii relativity nezávisí chod hodín len od ich relatívnej rýchlosti, ale aj od ich polohy (miesta) v gravitačnom poli. Hodiny na kopci idú pomalšie ako hodiny v údolí. Tento efekt je síce v pozemskom gravitačnom poli veľmi slabo badateľný, ale napríklad navigačný systém GPS ho zohľadňuje príslušnou úpravou frekvencie signálu, aby sa zabránilo chybám pri určovaní polohy.

[upraviť]Matematická štruktúra teórie

Kým špeciálnu teóriu relativity možno pochopiť aj s pomerne slabými znalosťami matematiky, je všeobecná teória relativity podstatne náročnejšia. Zakrivený časopriestor sa opisuje pomocou metód diferenciálnej geometrie, ktorá nahradila euklidovskú geometriu nám známeho plochého priestoru. Vznik zakrivenia sa opisuje pomocou einsteinovských rovníc poľa. Sú to diferenciálne rovnice tenzorového poľa s desiatimi zložkami, ktoré sú analyticky – čiže pomocou matematickej rovnice - riešiteľné len v špeciálnych prípadoch.

[upraviť]Kozmológia

Kým špeciálna teória relativity platí za prítomnosti hmotných telies len v oblastiach časopriestoru, ktoré sú také malé, že zakrivenie možno zanedbať, zaobíde sa všeobecná teória relativity bez tohto obmedzenia. Možno ju teda aplikovať aj na celý vesmír – preto hrá centrálnu úlohu v kozmológii. Napríklad rozpínanie vesmíru, ktoré pozorujú astronómovia, primerane opisujúfriedmannovské riešenia einsteinovských rovníc poľa v kombinácii s tzv. kozmologickou konštantou. Podľa nich začalo rozpínanie vesmíru veľkým treskom, ktorý sa podľa posledných výskumov udial pred 13,7 miliardami rokov, a ktorý možno chápať aj ako začiatok priestoru a času. Celý vesmír bol pritom skoncentrovaný na priestorovú oblasť s priemerom Planckovej dĺžky (cca. 1,61624·10^-35 m).

[upraviť]Čierne diery

Ďalšou predikciou všeobecnej teórie relativity sú čierne diery. Einsteinovi sa myšlienka čiernych dier vôbec nepozdávala a bol presvedčený, že musí existovať mechanizmus, ktorý zabraňuje vzniku takýchto objektov. Podľa súčasných pozorovaní však takéto objekty vo vesmíre skutočne existujú, a to ako konečné štádium vývinu hviezd pri veľmi hmotných hviezdach a v centrách väčšiny galaxií.

[upraviť]Gravitačné vlny

A napokon zo všeobecnej teórie relativity vyplýva existencia gravitačných vĺn, čiže lokálnych deformácií časopriestoru, ktoré sa šíria svetelnou rýchlosťou. Vznikať majú pri zrýchlení hmotných telies. Tieto deformácie sú však také malé, že sa ich dodnes nepodarilo priamo dokázať. Explózia supernovy v roku 1987 mala vytvoriť dokázateľné gravitačné vlny. Túto príležitosť storočia sme však prepásli, pretože v dôsledku chýbajúcej predchádzajúcej dohody boli všetky detektory gravitačných vĺn na celom svete v rozhodujúcich sekundách vypnuté z dôvodu údržby. Aspoň nepriamo sa gravitačné vlny podarilo dokázať z pozorovaní na sústavách dvojhviezd s pulzarmi.

[upraviť]Matematická formulácia všeobecnej teórie relativity

Všeobecná teória relativity (VTR) je teória gravitácie, času a priestoru. Na prvý pohľad nie je zrejmé, že tieto pojmy by mali byť opisované jedinou teóriou. Albert Einstein tento súvis geniálne rozoznal a popísal.

[upraviť]Filozofický základ VTR

V špeciálnej teórii relativity (ŠTR) sa postuluje rovnocennosť inerciálnych vzťažných sústav. To znamená, že fyzikálne zákony majú rovnaký matematický tvar pre všetkých pozorovateľov, ktorí sa pohybujú len zotrvačnosťou (stoja, alebo sa pohybujú rovnomerne priamočiaro). Táto požiadavka vedie k invariantnosti fyzikálnych zákonov voči Poincarého grupe. Einstein si položil otázku, prečo by mala príroda preferovať inerciálne sústavy. Zároveň si aj odpovedal: príroda sa o naše sústavy nestará, a preto musia byť zákony rovnaké pre všetkých pozorovateľov. Snažil sa preto zovšeobecniť ŠTR tak, aby mali fyzikálne zákony rovnaký matematický tvar pre všetkých pozorovateľov, inerciálnych aj zrýchlene sa pohybujúcich. To je základná myšlienka princípu relativity.

Veľkým skokom v Einsteinových úvahách bolo uvedomenie si, že pozorovateľ voľne padajúci v gravitačnom poli sa cíti byť inerciálny. Toto tvrdenie je známe ako princíp ekvivalencie. Znamená to, že pozorovateľ voľne padajúci v gravitačnom poli necíti zotrvačné sily a platí pre neho zákon zotrvačnosti. Dôležité je, že princíp ekvivalencie platí len lokálne, pretože pri nelokálnych meraniach sa uplatňujú nehomogenity gravitačného poľa.

[upraviť]Postuláty VTR

Princíp relativity požaduje, aby mali fyzikálne zákony rovnaký tvar vo všetkých sústavách. Každej vzťažnej sústave zodpovedá vhodná súradnicová sústava v priestoročase. To znamená, že fyzikálne zákony musia mať tvar rovnosti dvoch veličín, ktorá si pri zmene súradnicovej sústavy transformujú rovnako, takže rovnica si podrží svoju platnosť v každej sústave. Tejto požiadavke všeobecnej kovariancie vyhovujú tenzory a spinory.

V ŠTR je priestoročas hladkou varietou dimenzie 4, na ktorej je možné zaviesť globálne kartézske súradnice 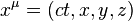$x^\mu = (c t, x, y, z)$ , v ktorých má metrický tenzor tvar

$\eta \;\;=\;\;c^2 {\rm d}t\otimes{\rm d}t\;-\;{\rm d}x\otimes{\rm d}x\;-\;{\rm d}y\otimes{\rm d}y\;-\;{\rm d}z\otimes{\rm d}z$

To je zmysel tvrdenia, že Minkowského priestoročas je plochý. Predpokladajme teraz, že v skutočnosti je priestoročas hladká varieta s nejakým všeobecným metrickým tenzorom. Na všeobecnej variete nemusia existovať vôbec žiadne globálne súradnice, tobôž nie kartézske. Metrický tenzor vyjadrený v ľubovoľných lokálnych súradniciach má tvar

$g \;\;=\;\; g_{\mu\,\nu}\;{\rm d}x^\mu\;\otimes{\rm d}x^\nu$

Podľa princípu ekvivalencie sa však vhodnou súradnicovou transformáciou dá dosiahnuť, že komponenty metrického tenzora sú v jednom bode dané diagonálnou maticou

$g_{\mu\,\nu}\;\;=\;\;{\rm diag}(1, -1, -1, -1)$ ,

čo znamená, že každý priestoročas je lokálne plochý. Pozorovateľ voľne padajúci v gravitačnom poli zistí, že lokálne platia zákony ŠTR. To, že metrický tenzor sa dá lokálne previesť na diagonálny kanonický tvar platí vo všeobecnosti na každej hladkej variete. To, že v priestoročase bude mať signatúru (+ - - -), je matematická formulácia princípu ekvivalencie. Ako uvidíme, Einsteinove rovnice gravitačného poľa sú diferenciálne rovnice pre metrický tenzor, ale jeho signatúra z nich nevyplýva. Často sa používa opačná signatúra (- + + +), alebo (+ + + -). Podstatné je len to, že časová zložka musí mať opačné znamienko ako priestorové. Signatúry s touto vlastnosťou sa nazývajú lorentzovské. Nami používaná signatúra (+ - - -) je bežne používaná napr. v kvantovej teórii poľa a má niekoľko výhod. Čo je však dôležitejšie, táto signatúra prirodzene vyplýva zo spinorovej formulácie teórie relativity.

Vlastným časom $\tau$ pozorovateľa nazývame čas, ktorý ukazujú hodiny, ktoré sú voči tomuto pozorovateľovi v pokoji. Pretože všetky merania je nutné robiť lokálne, predpokladáme, že poloha pozorovateľa a poloha hodín splývajú. Pri svojom pohybe v priestore opisuje pozorovateľ istú krivku v časopriestore. Túto krivku budeme nazývať svetočiara, čo je doslovný preklad anglického slova "worldline". Niekedy sa však aj slovo "geodetika" prekladá ako svetočiara, kým v tomto texte pojmom geodetika označujeme isté špeciálne svetočiary. Svetočiaru je možné ľubovoľne parametrizovať, zvoľme však ako parameter vlastný čas pozorovateľa $\tau$ . Ak svetočiaru označíme $\gamma$ , pohyb pozorovateľa je

$\gamma\;\;=\;\;\gamma(\tau)$

V ľubovoľných lokálnych súradniciach

$\gamma\;:\;x^\mu\;=\;x^\mu(\tau)\;\;,\;\;\;x^\mu(\tau)\;=\;x^\mu (\gamma(\tau) )$

Vektor $\dot{\gamma}$ dotykový k svetočiare označme $u$ . Jeho zložky sú

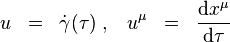
$u\;\;=\;\;\dot{\gamma}(\tau)\;,\;\;\;u^\mu\;\;=\;\;\frac{{\rm d}x^\mu}{{\rm d}\tau}$

Jeho norma je daná vzťahom

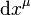$\left||u\right||^2\;\;=\;\;g(u,\;u)\;\;=\;\;g_{\mu\,\nu}\;\frac{{\rm d}x^\mu}{{\rm d}\tau}\;\frac{{\rm d}x^\nu}{{\rm d}\tau}$

Pritom ${\rm d}x^\mu$ je rozdiel súradníc dvoch bodov na svetočiare vzdialených o infinitezimálnu parametrickú vzdialenosť ${\rm d}\tau$ . Dĺžka svetočiary na tomto úseku je tzv. priestoročasový interval

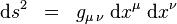
${\rm d}s^2\;\;=\;\;g_{\mu\,\nu}\;{\rm d}x^\mu\;{\rm d}x^\nu$

a teda

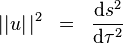
$\left||u\right||^2\;\;=\;\;\frac{{\rm d}s^2}{{\rm d}\tau^2}$

Táto veličina je invariant, a preto ju môžeme vyčísliť v ľubovoľných súradniciach. Predpokladajme, že 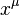$x^\mu$ sú súradnice pozorovateľa voľne padajúceho v gravitačnom poli. Potom časová súradnica je totožná s jeho vlastným časom, teda

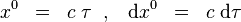
$x^0\;\;=\;\;c\;\tau\;\;,\;\;\;{\rm d}x^0\;\;=\;\;c\;{\rm d}\tau$

a pre ostatné súradnice

${\rm d}x^i\;\;=\;\;0\;,\;\;\;i\;=\;1,2,3$

Z toho

${\rm d}s^2\;\;=\;\;c^2\;{\rm d}\tau^2\;,\;\;$

Vidíme, že dĺžka svetočiary (priestoročasový interval) je len c-násobkom vlastného času. Norma štvorrýchlosti je potom

$\left||u\right||^2\;\;=\;\;c^2$

Pretože interval a vlastný čas sa líšia len o multiplikatívnu konštantu, môžeme svetočiaru rovnako dobre parametrizovať jej dĺžkou. V tom prípade je štvorrýchlosť bezrozmerná a normovaná na jednotku:

$\left||u\right||^2\;\;=\;\;g_{\mu\,\nu}\;\frac{{\rm d}x^\mu}{{\rm d}s}\;\frac{{\rm d}x^\nu}{{\rm d}s}\;\;=\;\;\frac{{\rm d}s^2}{{\rm d}s^2}\;\;=\;\;1$

V diferenciálnej geometrii sa takémuto parametru hovorí normálny. V teoretickej fyzike sa často volia jednotky, v ktorých sú fundamentálne konštanty (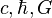 $c,\hbar,G$ ) rovné jednej. Potom časopriestorový interval a vlastný čas môžeme stotožniť.

[upraviť]Pohyb pokusnej častice v zadanom gravitačnom poli a lineárna konexia

Základná idea VTR je, že priestoročas je hladká varieta s lorentzovskou signatúrou. Geometria časopriestoru je zakódovaná v metrickom tenzore $g$ , a určuje ju rozloženie hmoty (všetkých jej foriem, teda látky aj polí). Prv, než budeme skúmať aký je presný vzťah medzi hmotou a geometriou, predpokladajme, že máme daný priestoročas s ľubovoľným fixným metrickým tenzorom. Zaujíma nás, ako sa bude v takomto priestoročase pohybovať pokusná častica. Samozrejme, prítomnosť tejto častice tiež ovplyvňuje výslednú geometriu, ale tento spätný vplyv predbežne zanedbajme. Uvidíme neskôr, že naše úvahy zostanú správne.

Nech svetočiara častice voľne padajúcej v gravitačnom poli je parametrizovaná jej vlastným časom, t. j. jej súradnice sú

$x^\mu\;\;=\;\;x^\mu(s)$

Sústava spojená s touto časticou je (lokálne) inerciálna. Predpokladajme, že 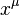$x^\mu$ sú lokálne geodetické súradnice spojené s časticou. Štvorrýchlosť má v týchto súradniciach zložky

$u^\mu\;\;=\;\;(1,0,0,0)$

pretože vlastný čas je totožný s časopriestorovým intervalom, t. j. ${\rm d}s=c{\rm d}t$ . Pretože sústava spojená s časticou je inerciálna, 4-rýchlosť častice sa pri pohybe pozdĺž svetočiary nemení, t. j. lokálne

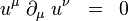
$u^\mu\;\partial_\mu\;u^\nu\;\;=\;\;0$

Toto nie je tenzorová rovnica, a platí len v uvažovaných súradniciach. Vieme však, že kovariantná súradnica sa v geodetických súradniciach redukuje na obyčajnú parciálnu deriváciu. Je preto prirodzené postulovať pre voľnú časticu pohybovú rovnicu

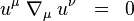
$u^\mu\;\nabla_\mu\;u^\nu\;\;=\;\;0$

alebo bezsúradnicovo

$\nabla_u\;u\;\;=\;\;0$

Je to rovnica geodetiky, a hovorí, že 4-rýchlosť musí byť paralelne prenášaná pozdĺž svetočiary. Na tejto úrovni sme teda postulovali, že voľná častica sa pohybuje po geodetike. Ako ale uvidíme, tento fakt je dôsledkom Einsteinových rovníc.

V tejto súvislosti musíme urobiť jednu poznámku. Pre bodovú časticu má bezsúradnicové vyjadrenie rovnice geodetiky dobre definovaný zmysel. Súradnicové vyjadrenie ale zahŕňa kovariantnú deriváciu vo všeobecnom smere 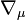$\nabla_\mu$ . Štvorrýchlosť bodovej častice je však definovaná len na svetočiare, preto jej derivácia vo všeobecnom smere nemá zmysel. Je preto užitočnejšie namiesto bodovej častice uvažovať kontinuum, tzv. koherentný prach, v ktorom jednotlivé "objemové elementy" neinteragujú, a teda sa chovajú ako voľné častice. Veličina $u$ je potom vlastne pole 4-rýchlosti kontinua, podobne ako pole rýchlosti v hydrodynamike. Takto budeme 4-rýchlosť naďalej chápať, hoci budeme pre jednoduchosť naďalej hovoriť o častici.

Dospeli sme zatiaľ k tomu, že voľná častica sa pohybuje po geodetike, čo znamená, že jej 4-rýchlosť (ktorá je vlastne dotykovým vektorom ku svetočiare) je paralelne prenášaná pozdĺž svetočiary. Sústavu spojenú s voľnou časticu nazývame geodetická sústava. Doposiaľ sme nešpecifikovali pravidlo paralelného prenosu. Toto pravidlo je technicky opisované lineárnou konexiou $\nabla$ , a musíme ho opäť postulovať. Predstavme si, že geodetický pozorovateľ sa nachádza v nejakom (infinitezimálne malom) laboratóriu a robí v ňom experimenty. Odmeria nejakú veličinu reprezentovanú 4-vektorom. Pretože celé laboratórium sa aj s pozorovateľom pohybuje po geodetike, tento 4-vektor je tiež paralelne prenášaný pozdĺž geodetiky. To znamená, že je kovariantne konšatný pri pohybe po geodetike. To však ešte nezaručuje, že jeho dĺžka sa nezmení, pretože konexia je v princípe od metriky nezávislá. Je preto prirodzené požadovať, aby sa dĺžky všetkých paralelne prenášaných 4-vektorov zachovávali. Nech $\gamma$ je geodetika, po ktorej sa častica pohybuje. Nech $V$ je 4-vektor paralelne prenášaný pozdĺž geodetiky, t. j.

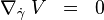
$\nabla_\dot{\gamma}\;V\;\;=\;\;0$

Požadujeme, aby jeho norma ostala pri geodetickom pohybe konštantná, t. j.

$\nabla_\dot{\gamma}\;\left||V\right||^2\;\;=\;\;\nabla_\dot{\gamma}\;g(V,V)\;\;=\;\;(\nabla_\dot{\gamma}g)(V,V)\;+\;2 g(V, \nabla_\dot{\gamma}V)\;\;=\;\;(\nabla_\dot{\gamma}g)(V,V)\;\;=\;\;0$

To bude splnené pre ľubovoľnú geodetiku len vtedy, ak samotný metrický tenzor bude kovariantne konštantný v ľubovoľnom smere. Postulujeme preto

$\nabla\;g\;\;=\;\;0$

Ak navyše predpokladáme, že konexia je symetrická, t. j. bez torzie, podmienka konštantnosti metrického tenzora už konexiu definuje jednoznačne. Takáto konexia sa nazýva metrická, alebo kompatibilná s metrikou, alebo RLC (Riemannova-Levi-Civitova). Predpoklad nulovosti torzie zdôvodníme za chvíľu. Lineárna konexia je určená Christoffelovými symbolmi. Nech $\partial_\mu$ je súradnicová báza vektorových polí. Christoffelove symboly sú definované vzťahom

$\nabla_\mu\;\partial_\nu\;\;=\;\;\Gamma_{\mu\,\nu}^\alpha\;\partial_\alpha$

Dá sa ľahko ukázať, že Christoffelove symboly RLC konexie majú nasledovné vyjadrenie:

$\Gamma^\alpha_{\mu\,\nu}\;\;=\;\;\frac{1}{2}\;g^{\alpha\,\beta}\;\left(\partial_\mu g_{\beta\,\nu}\;+\;\partial_\nu g_{\beta \,\mu}\;-\;\partial_\beta g_{\mu\,\nu}\right)$

Prechodom k lokálne geodetickej súradnicovej sústave možno docieliť, že všetky Christoffelove symboly budú v danom bode priestoročasu nulové. Je nutné poznamenať, že táto skutočnosť je jedným z prejavov toho, že Christoffelove symboly napriek trom indexom netvoria tenzor 3. rádu. Nenulový tenzor totiž nie je možné súradnicovou transformáciou vynulovať. A naopak, nulový tenzor ostáva nulový v každej sústave.

Geometrický význam Christoffelových symbolov je mnohoraký. V prvom rade, sú identicky nulové v kartézskom súradnicovom systéme v plochom priestore. Ale aj v plochom priestore sú nenulové v iných, než kartézskych súradniciach, napr. sférických. V tomto zmysle sú Christoffelove symboly mierou krivočiarosti súradnicového systému. Zdôrazňujeme, že priamo nesvedčia o zakrivenosti priestoru samotného. Je však možné z nich skonštruovať Riemannov tenzor krivosti. Tento tenzor je nulový v plochom priestore a nenulový v zakrivenom. Pretože je to tenzor, žiadnou transformáciou ho na zakrivenom priestore nemožno vynulovať, a to ani lokálne. Pre aparát VTR je dôležité, že Christoffelove symboly definujú pravidlo paralelného prenosu, a to cez kovariantnú deriváciu. Tá je pre vektorové pole $V$ daná nasledovne:

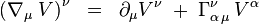
$\left(\nabla_\mu\;V\right)^\nu\;\;=\;\;\partial_\mu V^\nu\;+\;\Gamma^\nu_{\alpha\,\mu}\,V^\alpha$

Pre zjednodušenie zápisu zavedieme nasledujúcu, bežne používanú, konvenciu. Symbol $\nabla_\mu V$ znamená kovariantnú deriváciu vektora $V$ v smere bázového vektora $\partial_\mu$ . Výsledkom tejto operácie je vektor, ktorého $\nu$ -ta žložka je $\left(\nabla_\mu V\right)^\mu$ . Aby sme sa vyhli vypisovaniu zátvoriek, budeme jednoducho písať

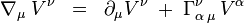
$\nabla_\mu\;V^\nu\;\;=\;\;\partial_\mu V^\nu\;+\;\Gamma^\nu_{\alpha\,\mu}\,V^\alpha$

Problém s týmto zápisom je ten, že prísne vzaté $V^\nu$ je skalárna funkcia (hoci označkovaná indexom) a jej kovariantná derivácia sa preto redukuje na parciálnu deriváciu, bez doplnkového člena s Christoffelovými symbolmi. Napriek tomu budeme túto konvenciu používať.

Aký je fyzikálny význam Christoffelových symbolov? Nech opäť $\gamma=\gamma(s)$ je geodetika parametrizovaná vlastným časom, nech 4-rýchlosť je

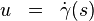
$u\;\;=\;\;\dot{\gamma}(s)$

Rovnica geodetiky je potom

$\nabla_u\;u\;\;=\;\;0$

Ak zavedieme ľubovoľné súradnice 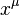$x^\mu$ , pričom

$x^\mu\;\;=\;\;x^\mu(s)\;,\;\;\;u^\mu\;\;=\;\;\frac{{\rm d}x^\mu}{{\rm d}s}$

súradnicové vyjadrenie rovnice geodetiky je

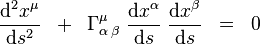
$\frac{{\rm d}^2 x^\mu}{{\rm d} s^2}\;\;+\;\;\Gamma^\mu_{\alpha\,\beta}\;\frac{{\rm d} x^\alpha}{{\rm d}s}\;\frac{{\rm d} x^\beta}{{\rm d}s}\;\;=\;\;0$

Ak túto rovnicu porovnáme s klasickou Newtonovou pohybovou rovnicou

$\frac{{\rm d}^2 x^i}{{\rm d} t^2}\;\;=\;\;F^i\;,$

kde $F^i$ je gravitačná sila, vidíme, že Christoffelove symboly hrajú v tejto analógii úlohu gravitačnej sily. Avšak, kým newtonovská gravitačná sila závisí len od polohy, do rovnice geodetiky vstupujú aj zložky 4-rýchlosti. Vieme, že pozorovateľ vo voľne padajúcej sústave nepociťuje gravitačnú silu. A skutočne, Christoffelove symboly sú v takejto sústave nulové. Tieto úvahy nás oprávňujú tvrdiť, že Christoffelove symboly naozaj reprezentujú gravitačnú silu. Pretože sú zostavené z derivácií metrického tenzora, môžeme povedať, že zložky metrického tenzora hrajú úlohu gravitačných potenciálov.

[upraviť]Tenzor krivosti

Ako sme už vysvetlili, lineárna konexia (reprezentovaná Christoffelovými symbolmi) priamo nepopisuje krivosť priestoru. Už preto nie, že Christoffelove symboly netvoria komponenty tenzora. Krivosť je charakterizovaná Riemannovým tenzorom krivosti (niekedy Riemannovým-Christoffelovým). Je to tenzor štvrtého rádu, a je definovaný vzťahom

$R(X,Y)Z\;\;=\;\;\nabla_X\;\nabla_Y\;Z\;-\;\nabla_Y\;\nabla_X\;Z\;-\;\nabla_{[X,Y]}Z$

V tomto definičnom vzťahu $R$ je Riemannov tenzor, 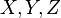$X,Y,Z$ sú ľubovoľné vektorové polia. Riemannov tenzor teda udáva komutátor kovariantných derivácií pri pôsobení na vektorové pole. Tretí člen na pravej strane je nutný, aby bol tenzor $R$ lineárny vo všetkých argumentoch. V skutočnosti v súradnicovej báze vypadne, keďže bázové vektorové polia indukované súradnicami komutujú. Súradnicovo potom posledná rovnica vyzerá nasledovne:

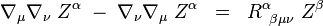
$\nabla_\mu\nabla_\nu\;Z^\alpha\;-\;\nabla_\nu \nabla_\mu \;Z^\alpha\;\;=\;\;R^\alpha_{\;\;\beta\mu\nu}\;Z^\beta$

Táto rovnosť sa nazýva aj Ricciho identita. Je zaujímavé, že v tetrádnom formalizme (spolu s Bianchiho identitou) nahradzuje Einsteinove rovnice poľa (napr. Newmanov-Penroseov formalizmus).

Pre nami uvažovanú metrickú konexiu sú komponenty Riemannovho tenzora voči súradnicovej báze nasledovné:

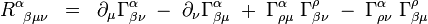
$R^\alpha_{\;\;\beta\mu\nu}\;\;=\;\;\partial_\mu\Gamma^\alpha_{\beta\nu}\;-\;\partial_\nu\Gamma^\alpha_{\beta\mu}\;+\;\Gamma^\alpha_{\rho\mu}\;\Gamma^\rho_{\beta\nu}\;-\;\Gamma^\alpha_{\rho\nu}\;\Gamma^\rho_{\beta\mu}$

Riemmanov tenzor (so spusteným indexom) spĺňa nasledovné identity:

$R_{\alpha\beta\mu\nu}\;\;=\;\;R_{[\alpha\beta][\mu\nu]}\;\;=\;\;R_{\mu\nu\alpha\beta}$

$R_{\alpha[\beta\mu\nu]}\;\;=\;\;0$

$\nabla_{[\rho}\;R_{\alpha\beta\mu]\nu}\;\;=\;\;0 \;\;\;\;{\rm Bianchiho\;\; identita}$

Pozrime sa teraz na fyzikálny význam tenzora krivosti. Ukážeme, že popisuje nehomogenity gravitačného poľa, tzv. slapové sily. Táto interpretácia je založená na Jacobiho rovnici pre deviáciu blízkych geodetík. Uvažujme kongruenciu geodetík, t. j. spojitú množinu geodetík takú, že každým bodom priestoročasu prechádza práve jedna geodetika, geodetiky sa nekrižujú (kongruenciu kriviek môžeme chápať ako zovšeobecnenie pojmu prúdnice v kvapaline). Nech $U$ je pole 4-rýchlostí, t. j. pole vektorov dotykových k tejto kongruencii, nech $\xi$ je vektorové pole "spájajúce" susedné geodetiky. Presná definícia znie, že integrálne krivky vektorového poľa $\xi$ prechádzajú tými bodmi kongruencie geodetík, na ktorých má rovnakú hodnotu parameter, ktorým sú geodetiky parametrizované. Platí

$\left[U,\xi\right]\;\;=\;\;0$ ,

teda tieto vektorové polia komutujú.

Predstavme si dvoch pozorovateľov na povrchu gule po geodetikách štartujúcich zo severného pólu a končiacich v južnom póle. Obaja títo pozorovatelia sú inerciálni, teda z pohľadu každého z nich sa pohybujú rovnomerne priamočiaro. Ak sa však pozrú jeden na druhého, zistia, že sa najprv vzďaľujú (až po rovník), a potom sa približujú (až po južný pól). Je zrejmé, že aj keď sú obaja pozorovatelia inerciálni, voči sebe sa nepohybujú rovnomerne - zrýchľujú a spomaľujú. Tento jav súvisí samozrejme s krivosťou variety, a preto by mal byť nejako opísaný Riemannovým tenzorom.

Uvažujme blízke geodetiky na ľubovoľnej variete spojené vektorom $\xi$ . Dotykové vektory týchto blízkych geodetík sa líšia o veličinu

$v\;\;=\;\;\nabla_\xi\;U$ ,

ktorú môžeme nazvať relatívnou rýchlosťou pozorovateľov pohybujúcich sa po týchto geodetikách. Táto rýchlosť sa pri pohybe mení, takže môžeme definovať relatívne zrýchlenie ako

$a\;\;=\;\;\nabla_U\;\nabla_\xi\;U$

Z definície Riemannovho tenzora, využijúc nulovosť komutátora polí $U,\xi$ , dostávame

$R(U,\xi)U\;\;=\;\;\nabla_U\;\nabla_\xi\;U\;\;-\;\;\nabla_\xi\;\nabla_U\;U$

Pretože uvažované krivky sú geodetiky, posledný člen je nulový, a prvý člen na pravej strane je nami definované zrýchlenie. Využijeme ešte znovu, že obe polia komutujú, takže dostaneme

$a\;\;=\;\;\nabla_U^2\;\xi\;\;=\;\;R(U,\xi)U$

Teda relatívne zrýchlenie blízkych geodetík je dané Riemannovým tenzorom krivosti. Ak si predstavíme fyzikálne laboratórium konečných rozmerov, teda nie infinitezimálne, voľne padajúce v gravitačnom poli, zistíme, že gravitačná sila je v rôznych bodoch laboratória rôzna. Geodetiky jednotlivých častí laboratória sa totiž vyznačujú relatívnym zrýchlením, čo zodpovedá nehomogenite poľa. Efektívne to zodpovedá existencii slapových síl.

[upraviť]Ricciho tenzor

Riemannov tenzor pripúšťa tri možné kontrakcie. Kontrakcia cez dvojicu indexov, v ktorých je tento tenzor antisymetrický dáva nulu, nenulové kontrakcie sa líšia len znamienkom. Symetrický Ricciho tenzor druhého rádu definujeme ako

$R_{\mu\nu}\;\;=\;\;R^\alpha_{\;\;\;\mu\alpha\nu}$

Jeho stopa sa nazýva skalárna krivosť:

$R\;\;=\;\;R^\alpha_\alpha$

Kontrakciou Bianchiho identít dostávame dôležitý vzťah pre kovariantnú divergenciu Ricciho tenzora

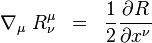
$\nabla_\mu\;R^\mu_\nu\;\;=\;\;\frac{1}{2}\frac{\partial R}{\partial x^\nu}$

Ricciho tenzor je pre VTR dôležitý z týchto dôvodov. Je to tenzor druhého rádu, rovnako ako tenzor energie-hmotnosti, ktorý popisuje rozloženie hmoty v priestoročase. Je funkciou metrického tenzora a jeho derivácií, pričom je lineárny v druhých deriváciách. Od novej teórie musíme požadovať, aby v klasickej limite dávala rovnaké výsledky ako stará úspešná teória. Newtonov gravitačný zákon je ekvivalentný Poissonovej rovnici, v ktorej sa vyskytuje Laplaceov operátor pôsobiaci na gravitačný potenciál. Vieme už, že analógiou gravitačného potenciálu vo VTR sú komponenty metrického tenzora. Preto sa VTR musí v klasickej limite redukovať na Poissonovu rovnicu pre metrický tenzor. Ak predpokladáme, že geometria priestoročasu je daná rozložením hmoty, znamená to, že tento vzťah musí byť vyjadrený ako rovnosť tenzora energie hybnosti, a nejakého tenzora druhého rádu, ktorý obsahuje druhé derivácie metrického tenzora, a to lineárne. Ricciho tenzor je zjavne veľmi dobrým kandidátom.

[upraviť]Tenzor energie-hybnosti

tenzor energie-hybnosti je známy už zo ŠTR. Je to tenzor charakterizujúci kontinuum a má nasledovnú štruktúru:

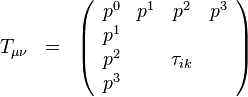
$T_{\mu\nu}\;\;=\;\; \left(\begin{array}{cccc} p^0 & p^1 & p^2 & p^3 \\ p^1 & ~ & ~ & ~ \\ p^2 & ~ & \tau_{ik}& ~ \\ p^3 & ~ & & ~ \end{array}\right)$

V tomto zápise $p^\mu,\mu=0,1,2,3,4$ je hustota štvorhybnosti kontinua, a $\tau_{ik}, i,k=1,2,3$ je jeho trojrozmerný tenzor napätia známy z elementárnej mechaniky kontinua. Tenzor energie-hybnosti však možno zovšeobecniť aj na nelátkové kontinuum, teda na polia. Pozrime sa, ako sa definuje tento tenzor v ŠTR vo všeobecnosti.

Minkowského plochý priestoročas sa vyznačuje symetriou voči Poincarého grupe transformácií. Táto grupa pozostáva z translácií (nehomogénna časť Poincarého grupy) a Lorentzových transformácií (homogénna časť, tzv. Lorentzova grupa). Lorentzova grupa pozosáva z priestorových trojrozmerných rotácií a z tzv. boostov (niekedy hyperbolickýc rotácií). Boosty sú rotácie v rovine určenej jedným časupodobným a jedným priestorupodobným vektorom. Všeobecná Poincarého transformácia má tvar

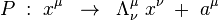
$P\;:\;x^\mu\;\;\rightarrow\;\;\Lambda^\mu_{\nu}\;x^\nu\;+\;a^\mu$

kde 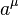$a^\mu$ je translačný 4-vektor a $\Lambda^\mu_\nu$ je matica Lorentzovej transformácie. Je to matica, pre ktorú platí

$\Lambda^T\;\eta\;\Lambda\;\;=\;\;\eta$

kde $\eta$ je kanonický Minkowského metrický tenzor.

To, že Minkowského priestor je invariantný voči Poincarého grupe znamená, že jeho najvšeobecnejší Killingov vektor je

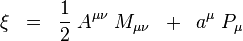$\xi\;\;=\;\;\frac{1}{2}\;A^{\mu\nu}\;M_{\mu\nu}\;\;+\;\;a^\mu\;P_\mu$ ,

kde 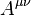$A^{\mu\nu}$ je antisymetrická matica a

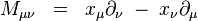
$M_{\mu\nu}\;\;=\;\;x_\mu\partial_\nu\;-\;x_\nu\partial_\mu$

$P_\mu\;\;=\;\;\partial_\mu$

sú generátory rotácií (hyperbolických aj priestorových) a translácií. V kvantovej mechanike by sme povedali, že sú to operátory momentu hybnosti a hybnosti (až na faktor 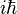$i\hbar$ ).

Táto invariancia sa slovne formuluje tak, že Minkowského priestor je homogénny (invariantný voči transláciám) a izotropný (invariantný voči rotáciám). To ale znamená, že akákoľvek izolovaná sústava musí mať tie isté symetrie. Pre dobrú predstavu uvažujme izolovanú mechanickú sústavu. Je zrejmé, že nezáleží na tom, v ktorom mieste priestoru sa nachádza, jej časový vývoj musí byť rovnaký. Napr. plyn uzavretý v nádobe s danou vnútornou energiou bude mať rovnaký tlak na Zemi, či v súhvezdí Andromédy (ak zanedbáme pôsobenie gravitácie). To je invariantnosť voči translácii v priestore. Takisto je jedno, či experiment budeme robiť v pondelok, alebo v sobotu popoludní. Fyzikálne zákony sa (veríme) nemenia s časom, takže izolovaná sústava musí byť invariantná voči translácii v čase. Tým sme vyčerpali translácie. Ak si navyše uvedomíme, že nazáleží ani na tom, ako nádobu v priestore natočíme, ani na tom, či nádobu skúma jeden inerciálny pozorovateľ, alebo takú istú nádobu vo svojej rakete iný pozorovateľ, môžeme konštatovať, že izolovaná sústava musí byť invariantná voči Lorentzovým transformáciám.

Sformulujme to matematicky. Nech $L$ je hustota lagrangiánu sústavy charakterizovanej poľom $\phi$ . Toto pole v skutočnosti môže mať viac komponentov, ktoré pre jednoduchosť nevypisujeme. Lagrangián je funkciou samotného poľa a všetkých jeho derivácií, teda gradientu. Účinok sústavy

$S\;\;=\;\;\int\;L(\phi,{\rm d}\phi)\;{\rm d}^4 x$

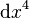je invariantný voči transformácii generovanej vektorom $\xi$ uvedenom vyššie. Symbolom ${\rm d}x^4$ sme tu označili objemový element časopriestoru v kartézskych súradniciach. Podotýkame, že tento objemový element je invariantný voči Poincarého transformáciám, pretože do diferenciálu nevstupuje konštantný translačný vektor, a ako vyplýva z definície Lorentzovej matice, jej determinant je v absolútnej hodnote rovný jednej.

Požiadavka invariancie účinku voči transláciám vedie k rovnici

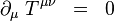
$\partial_\mu\;T^{\mu\nu}\;\;=\;\;0$

kde

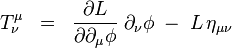
$T^\mu_\nu\;\;=\;\;\frac{\partial L}{\partial \partial_\mu \phi}\;\partial_\nu\phi\;-\;L\,\eta_{\mu\nu}$

je tzv. kanonický tenzor energie-hybnosti. Nulovosť jeho štvordivergencie predstavuje rovnicu kontinuity, lokálny zákon zachovania. Podobne, požiadavka invariancie účinku voči Lorentzovým transformáciám vedie k zachovaniu tenzora momentu hybnosti

$M^{\rho\mu\nu}\;\;=\;\;x^\mu T^{\rho\nu}\;-\;x\nu T^{\rho\mu}\;\;.$

Kanonický tenzor energie-hybnosti nie je vhodný pre VTR. Z jeho definície napr. vôbec nie je zrejmé, že je symetrický. Navyše, toto vyjadrenie sa nedá priamočiaro zovšeobecniť pre zakrivený priestor.

Vo VTR neexistuje preferovaná grupa transformácií, pretože povolené sú všetky súradnicové transformácie. To, čo potrebujeme, je získať z účinku pre hmotu symetrický tenzor druhého rádu, ktorý sa bude zachovávať, t. j. jeho kovariantná divergencia bude nulová. Riešenie je prekvapivo elegantné a hlboké.

V teórii (akýchkoľvek) transformácií býva zmienka o rozdieli medzi aktívnymi a pasívnymi transformáciami. Pasívne sú tie, pri ktorých nemeníme skúmanú štruktúru, ale súradnicovú sústavu, v ktorej ju opisujeme. Pri aktívnych transformáciách naopak nemeníme súradnice, ale transformujeme objekt, ktorý popisujeme. Oba pohľady sú úplne ekvivalentné, a záleží len na interpretácii v tom-ktorom konkrétnom prípade.

Súradnicová zámena na variete je zjavne typická pasívna transformácia. Môžeme ju interpretovať tak, že priestoročas (skúmaný objekt) je objektívny a nezávislý na tom, ako ho pozorujeme. Realita je len jedna, ale rôzni pozorovatelia ju môžu vnímať rôzne. Akonáhle si zvolíme jedného konkrétneho pozorovateľa, definujeme tým súradnicový systém. Zvolíme si druhého pozorovateľa, definujeme druhý súradnicový systém. Je však zrejmé, že samotný priestoročas na súradniciach nezávisí, a tranformácia z jedných súradníc do druhých nemá nijaký vplyv na vlastnosti priestoročasu samotného.

Nech 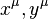$x^\mu,y^\mu$ sú dva súradnicové systémy majúce spoločnú oblasť platnosti. V tejto oblasti pod súradnicovou zámenou rozumieme zobrazenie

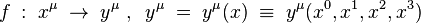$f\;:\;x^\mu\;\rightarrow\;y^\mu\;,\;\;y^\mu\;=\;y^\mu(x)\;\equiv\;y^\mu(x^0, x^1, x^2, x^3)$ ,

ku ktorému existuje zobrazenie inverzné

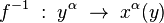
$f^{-1}\;:\;y^\alpha\;\rightarrow\;x^\alpha (y)$

Pravidlo pre transformáciu zložiek vektorového poľa nájdeme jednoducho:

$V(x)\;\;=\;\;V^\mu(x)\;\frac{\partial}{\partial x^\mu}\;\;=\;\;V^\mu(x(y))\;\frac{\partial y^\alpha}{\partial x^\mu}\;\frac{\partial}{\partial y^\alpha}\;\;\rightarrow\;\;V^\alpha (y)\;\;=\;\;\frac{\partial y^\alpha}{\partial x^\mu}\;V^\mu(x(y))$

Aj tu je ale možná aktívna interpretácia. Zobrazenie $f$ môžeme chápať ako transformáciu (difeomorfizmus) variety samej na seba, ktorá zobrazí bod so súradnicami $x$ do bodu so súradnicami $y$ . Tým sa transformujú aj všetky tenzorové polia, pričom tranformačný zákon je formálne úplne rovnaký ako pri súradnicovej zámene. Preto dve difeomorfné variety považujeme vo VTR za ekvivalentné (relácia "byť difeomorfný" je reláciou ekvivalencie v matematickom zmysle). Keďže podľa princípu relativity všetky súradnicové systémy sú fyzikálne rovnako dobré, znamená to, že difeomorfné variety popisujú presne ten istý priestoročas, len v iných súradniciach. Fyzikálne výsledky musia byť rovnaké pre všetky difeomorfné priestoročasy. Tomuto tvrdeniu (alebo iným jeho formám) sa hovorí princíp všeobecnej kovariancie.

V ŠTR sme zákony zachovania formulovali na základe invariancie voči Poincarého grupe. Vo VTR sme spočiatku nevideli nejakú preferovanú grupu, ale teraz vieme, že teória musí byť invariantná voči difeomorfizmom. Túto požiadavku teraz sformulujeme matematicky, a bez detailného odvodenia (viac pozri v hlavnom článku Tenzor energie-hybnosti) ukážeme, že vedie k zachovaniu veličiny, ktorú nazveme tenzor energie-hybnosti.

V ŠTR je objemový element invariantný voči Poincarého transformáciám, ale nie je invariantný voči ľubovoľnej súradnicovej transformácii, ale transformuje sa cez Jacobián príslušnej transformácie. Definujme formu objemu asociovanú s metrickým tenzorom

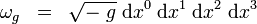
$\omega_g\;\;=\;\;\sqrt{-\;g}\;{\rm d}x^0\;{\rm d}x^1\;{\rm d}x^2\;{\rm d}x^3$

Symbolom $g$ tu označujeme determinant metrického tenzora. Forma objemu predstavuje to, čo sa bežne nazýva objemový element, ale je to tenzor voči ľubovoľným transformáciám. Jej význam je nasledovný: ak za jej argumenty dosadíme ľubovoľné 4 vektory z dotykového priestoru, jej hodnota predstavuje objem rovnobežnostena natiahnutého na tieto vektory. Nech negravitačná hmota (látka a negravitačné polia) je popísaná poľom $\phi$ . Účinok negravitačnej hmoty má tvar

$S_M[\phi,g]\;\;=\;\;\int_D\;L(\phi, g)\;\omega_g$

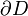kde $D$ je 4-rozmerná oblasť s hranicou $\partial D$ . Lagrangián je funkciou metrického tenzora, pretože sa v ňom vyskytujú rôzne kontrakcie. Označme