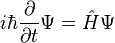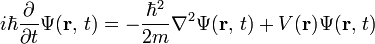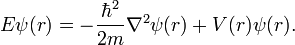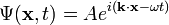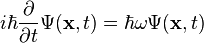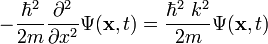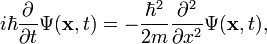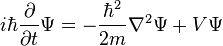Schoningerova rovnica

13.11.2012 20:53

 

Schrödingerova rovnica je základná diferenciálna rovnica, ktorá určuje vývoj fyzikálneho systému formalizmom vlnovej mechaniky. Je ústrednou rovnicou kvantovej mechaniky. Pomenovaná je podľa Erwina Schrödingera, ktorý ju sformuloval v roku 1926.[chýba zdroj]

Schrödingerova rovnica môže byť matematicky pretransformovaná na Heisenbergovu maticovú mechaniku a Feynmanovu formuláciu dĺžkového integrálu.

Schrödingerova rovnica

V závislosti od toho, aký systém chceme popísať, Schrödingerovu rovnicu môžeme napísať vo viacerých tvaroch. V tejto časti predstavujeme rovnicu pre všeobecné a jednoduché prípady, ktoré sú predmetom mnohých učebníc.

[upraviť]Všeobecný kvantový systém

Pre všeobecný kvantový systém platí:[1]

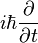i\hbar\frac{\partial}{\partial t} \Psi = \hat H \Psi

kde

[upraviť]Jedna častica s potenciálnou energiou

Pre jednu časticu, na ktorú pôsobia sily (čiže potenciálna energia V je nenulová), má Schrödingerova rovnica tvar:[3]

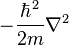i\hbar\frac{\partial}{\partial t} \Psi(\mathbf{r},\,t) = -\frac{\hbar^2}{2m}\nabla^2\Psi(\mathbf{r},\,t) + V(\mathbf{r})\Psi(\mathbf{r},\,t)

kde

  • -\frac{\hbar^2}{2m}\nabla^2 je operátor kinetickej energie (m je hmotnosť častice),
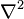  • \nabla^2 je Laplaceov operátor. V troch rozmeroch má Laplaceov operátor tvar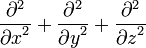\frac{\partial^2}{{\partial x}^2} + \frac{\partial^2}{{\partial y}^2} + \frac{\partial^2}{{\partial z}^2}, kde x, y a z sú osi v karteziánskej súradnicovej sústave,
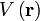  • V\left(\mathbf{r}\right) je časovo nemenná potenciálna energia v mieste udanom polohovým vektorom r,
  • \Psi(\mathbf{r},\,t) je amplitúda pravdepodobnosti pre časticu, ktorá sa má nachádzať v čase t na mieste určenom polohovým vektorom r.

[upraviť]Časovo nezávislá Schrödingerova rovnica

Časovo nezávislá Schrödingerova rovnica pre jednu časticu s potenciálnou energiou V má tvar:[4]

{E}\psi(r) = - {\hbar^2 \over 2m} \nabla^2 \psi(r) + V(r) \psi(r).

[upraviť]Odvodenie

[upraviť]Krátke heuristické odvodenie

Schrödingerova rovnica môže byť odvodená nasledovným spôsobom.[chýba zdroj]

[upraviť]Predpoklady

  1. Celková energia častice E je
    E = T + V = \frac{p^2}{2m}+V.
    Toto je klasický zápis pre časticu s hmotnosťou m, kde celková energia E je daná súčtom kinetickej energie T a potenciálnej energie V (táto sa môže meniť v závislosti od polohy a času). p je hybnosť častice a m jej hmotnosť.
  2. Einsteinova hypotéza kvánt energie z roku 1905, podľa ktorej je energia E fotónu priamoúmerná veľkosti frekvencie ν (alebo uhlovej frekvencie ω = 2πν) korešpondujúcej elektromagnetickej vlny.
    E = h\nu = \hbar \omega \;,
  3. de Broglieho hypotéza z roku 1924, podľa ktorej akejkoľvek častici môže byť priradená vlna a hybnosť častice p je vo vzťahu ku vlnovej dĺžke λ (alebo vlnového čisla k) takom, že platí:
    p = \frac{h}{\lambda} = \hbar k\;,
  4. Tieto tri predpoklady umožňujú odvodiť len rovnicu pre rovinnú vlnu. Tvrdiť, že takáto rovnica platí pre akúkoľvek vlnu vyžaduje princíp superpozicie, a preto je nutné postulovať nezávislý predpoklad, že Schrödingerova rovnica je lineárna.

[upraviť]Vyjadrenie vlnovej funkcie vo forme komplexnej rovinnej vlny

Hľadáme parciálnu diferenciálnu rovnicu, ktorej riešením je nasledovná rovnica pre rovinnú vlnu (i):

\Psi(\mathbf{x},t) = Ae^{i(\mathbf{k}\cdot\mathbf{x}- \omega t)}
kde A je komplexná konštanta

Platí:

E = \frac{p^2}{2m}

Použijúc druhý a tretí predpoklad dostávame (ii):

\hbar\omega = {\hbar^2\ k^2\over 2m}

Teraz zderivujeme vlnovú funkciu (i) najskôr podľa času t a potom podľa osi x:

i\hbar\frac{\partial}{\partial t} \Psi (\mathbf{x},t) = \hbar\omega \Psi (\mathbf{x},t)

 

-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} \Psi (\mathbf{x},t) = {\hbar^2\ k^2\over 2m} \Psi (\mathbf{x},t)


Keďže platí (ii), platí aj

 

i\hbar\frac{\partial}{\partial t} \Psi (\mathbf{x},t) = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} \Psi (\mathbf{x},t),


čo je Schrödingerova rovnica pre časticu pohybujúcu sa v smere osi x za neprítomnosti potenciálu V.

Schrödingerova rovnica pre časticu v trojrozmernom priestore za prítomnosti pôsobenia síl (teda potenciálu V) má tvar:

 

i\hbar\frac{\partial}{\partial t}\Psi=-\frac{\hbar^2}{2m}\nabla^2\Psi + V\Psi
Späť